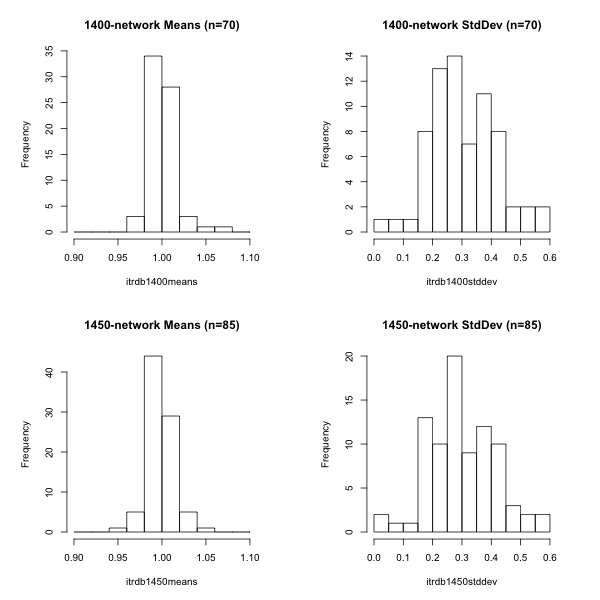
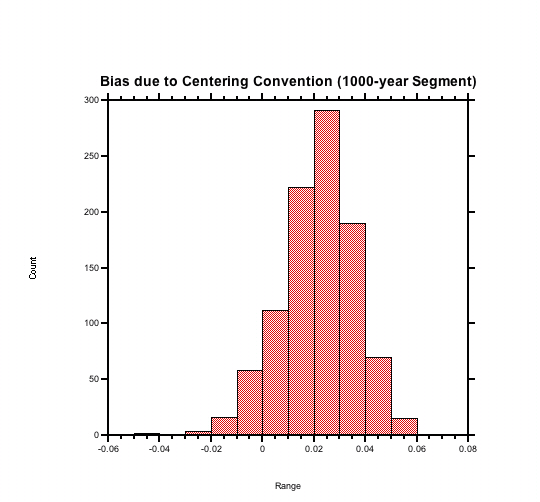
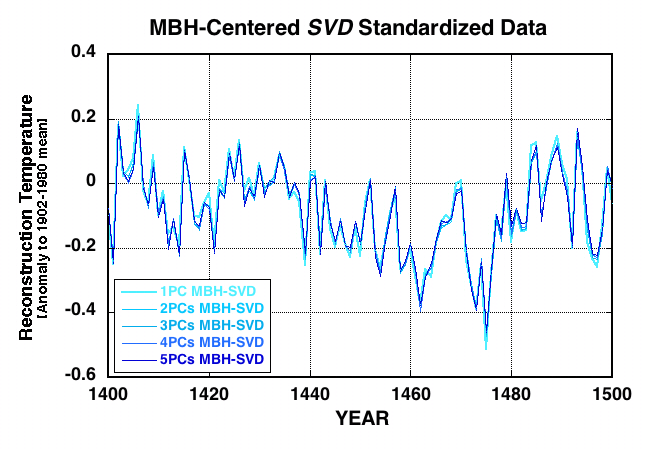
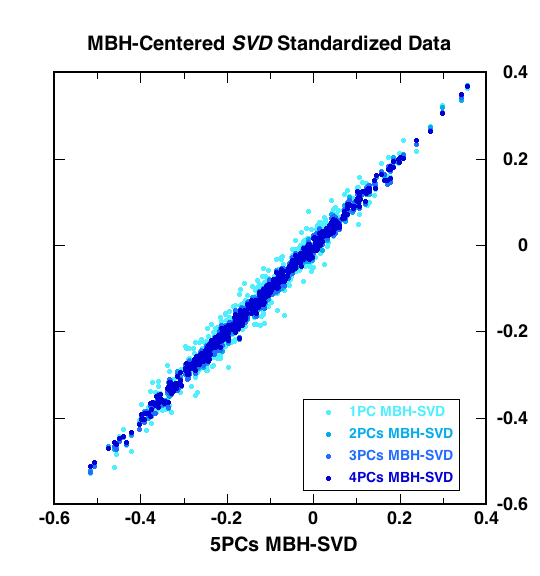
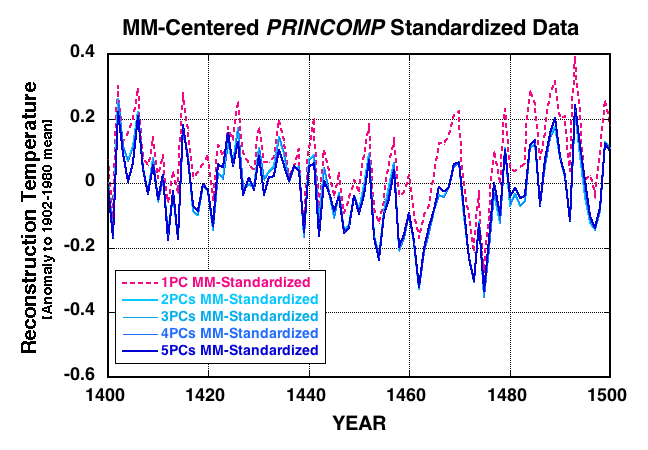
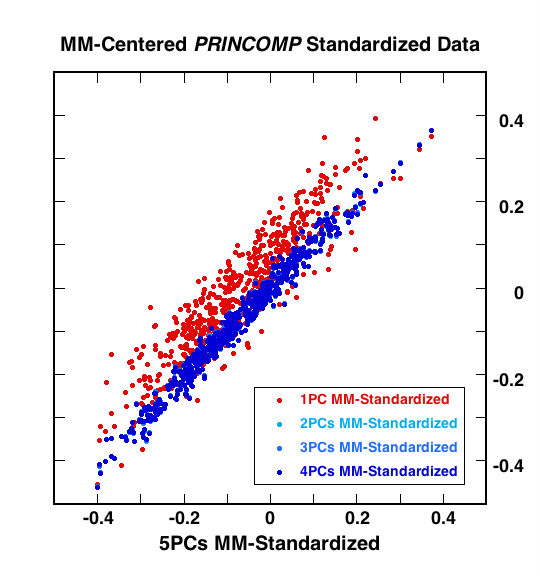
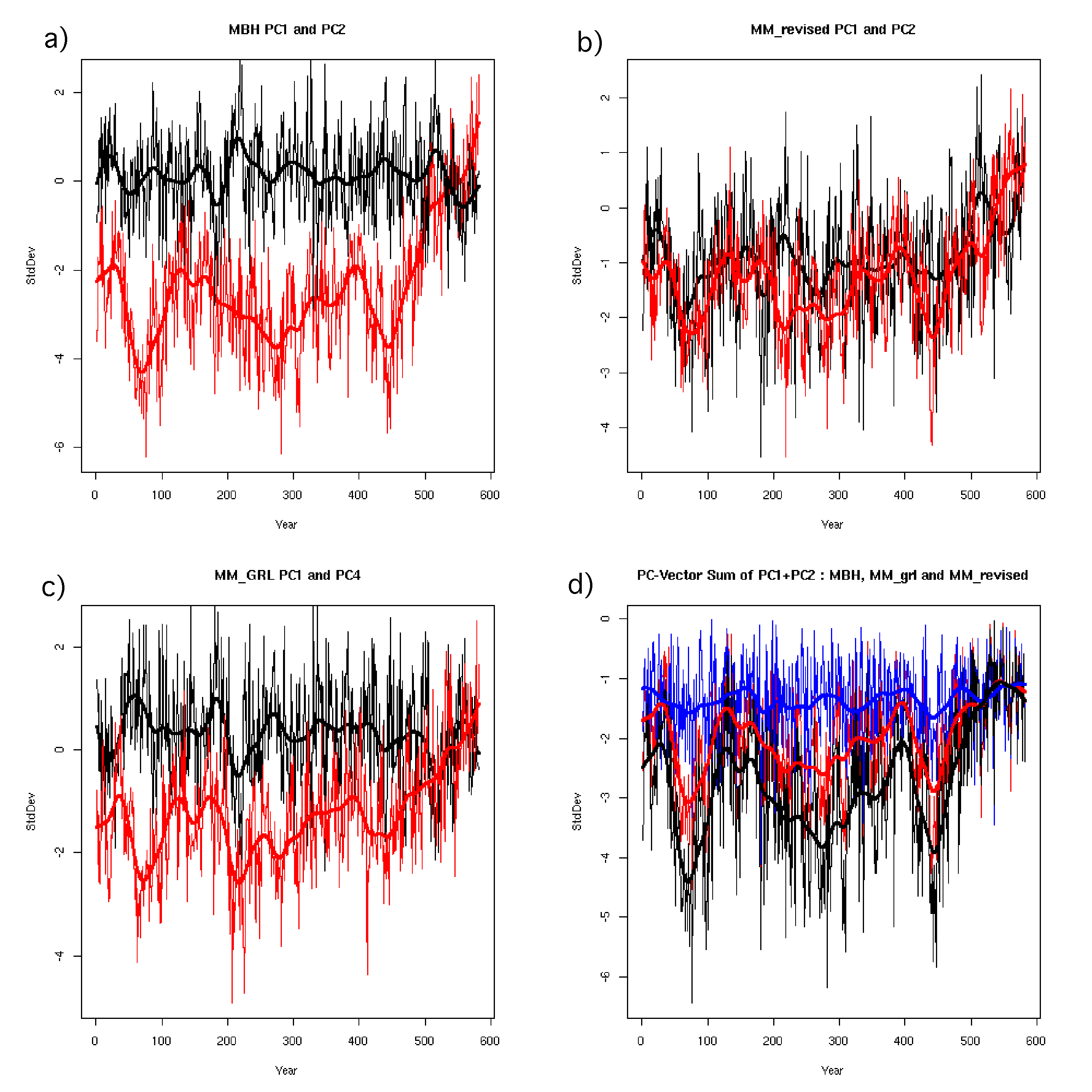
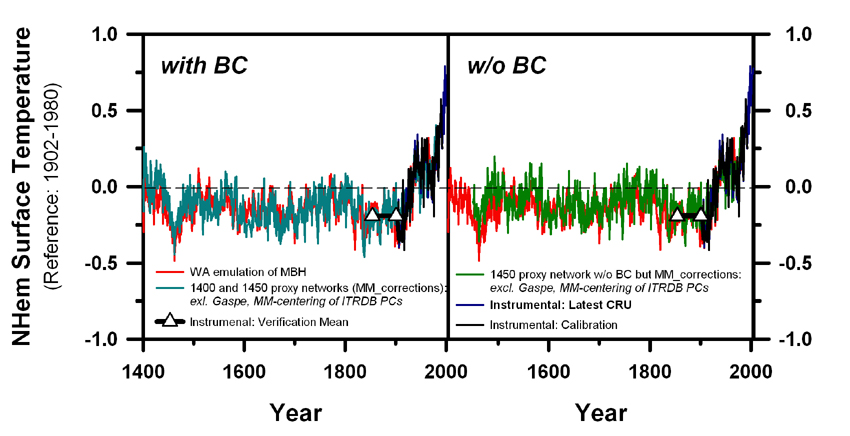
| Figure 1 | Figure 2: Correction of MBH (full long-term centering) |
|---|---|
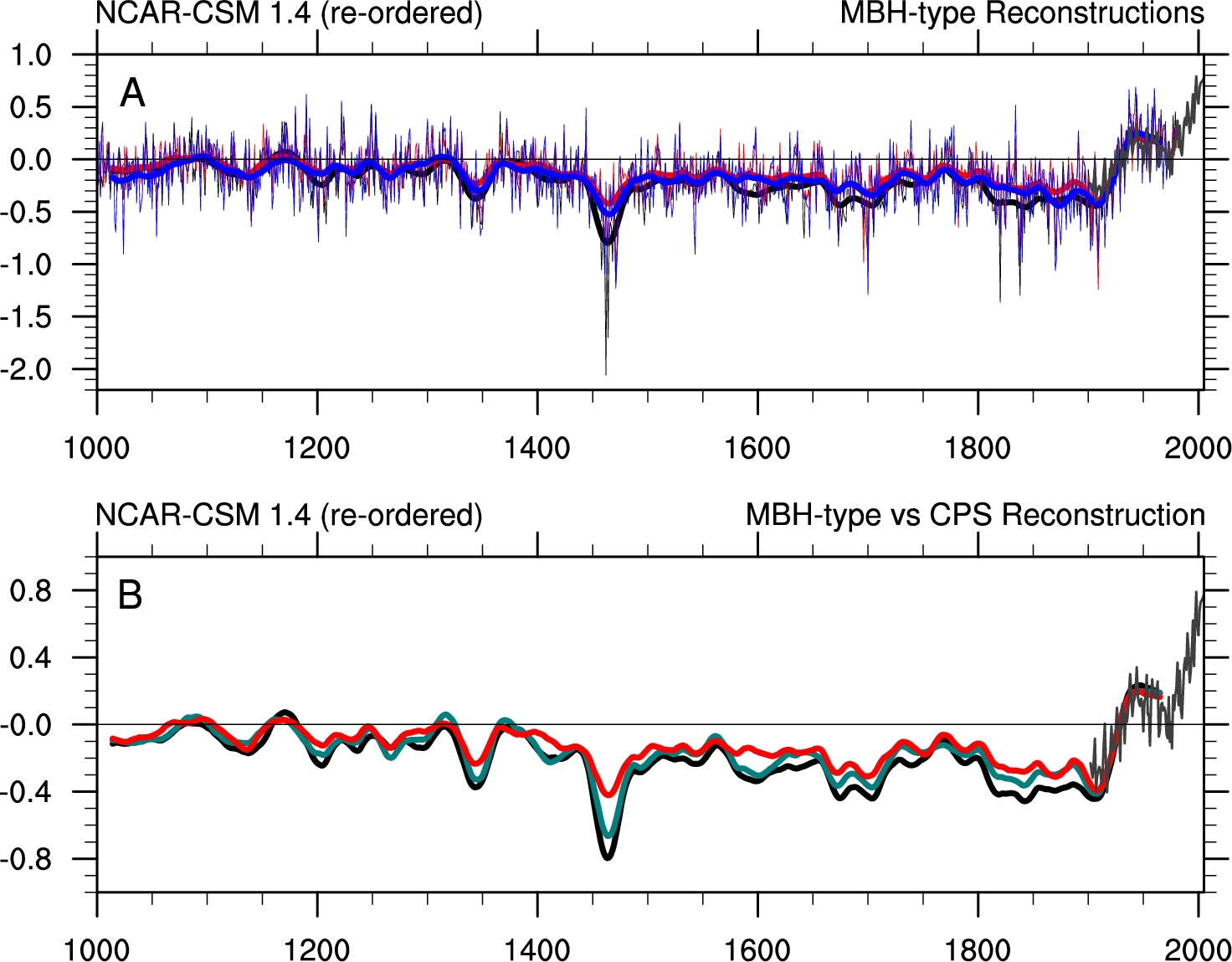
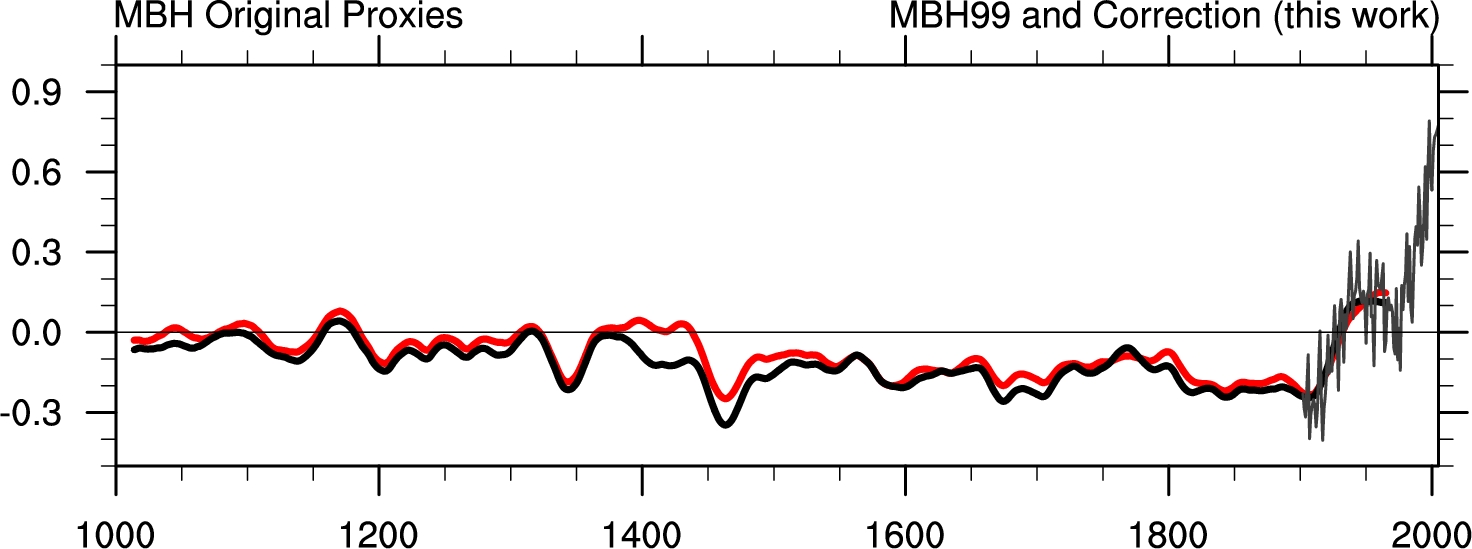
| 
|
| Figure 1 | Figure 2: Correction of MBH (full long-term centering) |
|---|---|

| 
|
| | |
|---|---|
 |
 |
 |
 |
 |
 |
| Proxy Network (WA-emulation of MBH 1998) | RE Significance Level | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1400-network | | 1450-network | 1500-network | 1600-network | 1700-network | 1730-network | 1750-network | 1760-network | 1780-network | 1800-network | 1820-network | |
| MBH-1999/WA-emulation of 1000-year network | RE-Significance Level |
|---|---|
| noCO2 correction, full-period-centered proxy PCs |
| MBH-Network | WA-Scenarios and Signifiance Levels | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5a | 5b | 5c | 5d | 6a | 6b | 6c | |||||||||
| 1400 | 0.94 | 0.77 | 0.74 | 0.26 | 0.31 | 0.27 | 0.27
| 1450 | 0.95 | 0.97 | 0.96 | 0.96 | 0.96 | 0.95 | 0.93
| |